Aufgabe 1:
Sei im Folgenden 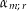 die Kreiskurve mit Mittelpunkt
die Kreiskurve mit Mittelpunkt 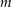 und Radius
und Radius  . Es sei also
. Es sei also ![$\curve mr :\ \left[0,\,1\right]\rightarrow\C:\ t\mapsto m+r\cdot\exp\left(2\pi t \i\right)$](img/92_937226401_06060006080105a5a30805a50803a300.png) . Berechne nun folgende Kurvenintegrale:
. Berechne nun folgende Kurvenintegrale:
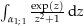 (keine Definitionslücken innerhalb der zu integrierenden Kurve)
(keine Definitionslücken innerhalb der zu integrierenden Kurve) 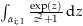 (eine Definitionslücke innerhalb der zu integrierenden Kurve)
(eine Definitionslücke innerhalb der zu integrierenden Kurve) 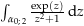 (mehrere Definitionslücken innerhalb der zu integrierenden Kurve)
(mehrere Definitionslücken innerhalb der zu integrierenden Kurve)